Jeder kennt mit Sicherheit die verschiedenen bergrauf… bergrunter –Sprüche aus der Jägerschaft. In der jagdlichen Welt existiert darüber sehr viel gefährliches Halbwissen und gern wird am Stammtisch so manches „Wissen“ herumgereicht. Genau betrachtet, basiert der Schuss im Winkel jedoch auf einfachen physikalischen Grundlagen. Im folgenden Artikel möchten wir mit dem Mythos Winkelschuss aufräumen und die Schießlehre für den Schuss in steilen Winkeln erklären.
Im Grunde genommen ist Schießen in der Theorie nicht schwer, denn es ist reine Physik und basiert auf mathematischen Grundsätzen, die jedem hinlänglich aus der Schule bekannt sein müssten. Mit dem Winkelschuss ist dies natürlich genauso:
Es gibt mehrere Modelle zur Erklärung des steilen Schuss. Die populärste Theorie, auf der auch die meisten Ballistikrechner basieren ist die Rifleman-Rule oder Sniperchoice. Diese besagt, bei einem Winkelschuss verkürzt man die Strecke auf der die Schwerkraft auf das Projektil einwirken kann, wodurch das Geschoss eine kürzere Strecke fliegt. Am besten kann man sich dieses physikalische Phänomen veranschaulichen, wenn man zu Hause den Gartenschlauch nimmt und in unterschiedlichen Winkeln das Beet bewässert. Man wird feststellen, dass bei einem Winkel von 45° das Wasser am weitesten spritzt und das Wasser in einer parabelförmigen Flugbahn seinen Weg nimmt. Die relative Entfernung am Boden, die das Wasser dabei zurück legt, ist daber stehts kürzer als die Strecke der Flugbahn.
Grundlagen
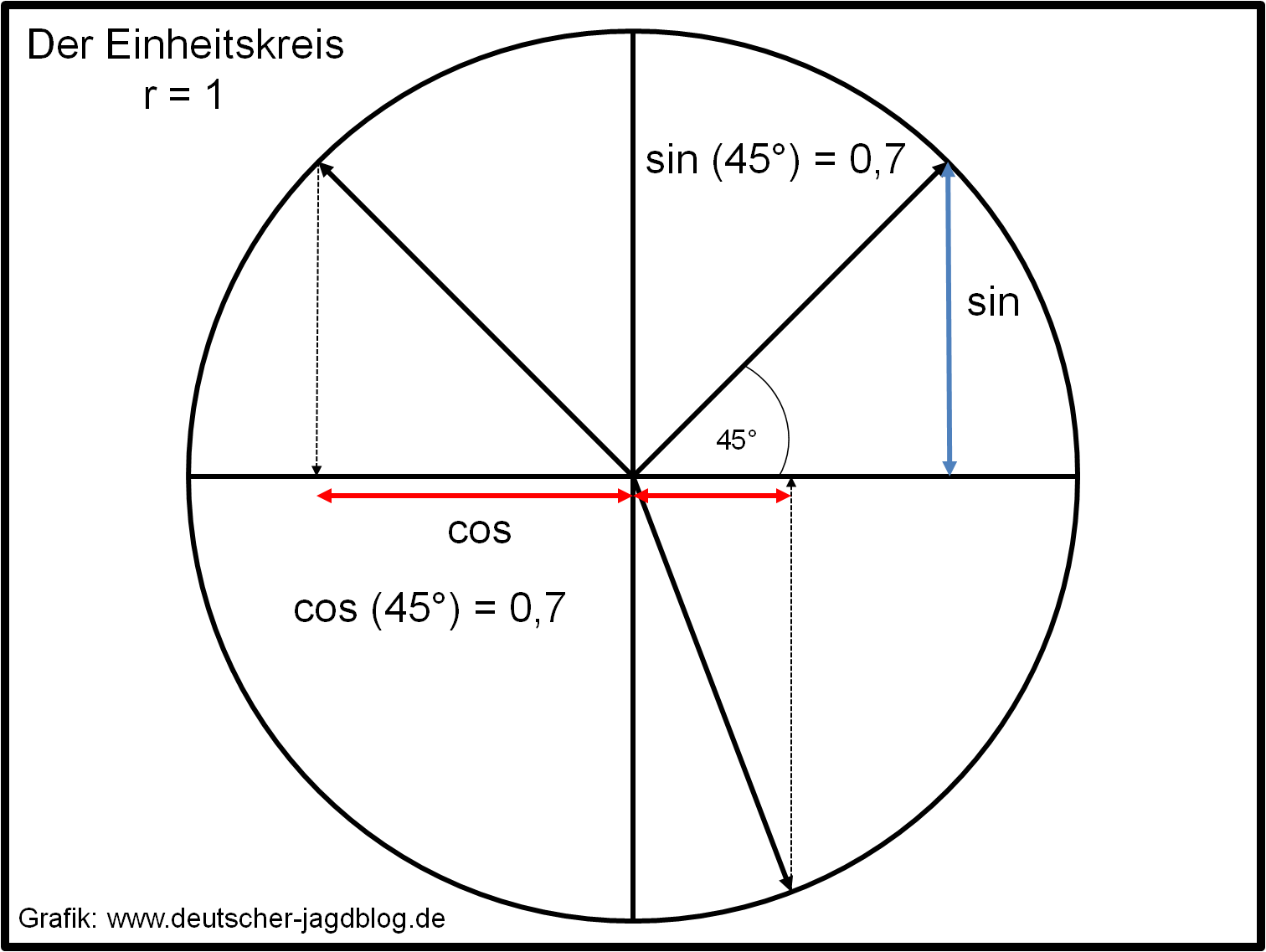
Am einfachsten lässt sich der Winkelschuss mit dem mathematischen Einheitskreis erklären. Keine Sorge wir werden die Berechnung des Sinus und Cosinus nicht herleiten – wir setzen einfach mal voraus, dass jeder grundlegend mit der Thematik vertraut sein sollte. Zudem setzen wir die Grundkenntnisse über die Außenballistik voraus, die wir für die weitere Betrachtung ausklammern werden.
Der mathematische Einheitskreis ist ein größenunabhängiger Kreis mit dem Radius 1. Auf der Abbildung 1 haben wir zur Veranschaulichung einen solchen Kreis gezeichnet und in vier Teile unterteilt. Zieht man nun eine Verbindung vom Mittelpunkt des Kreises zur Außenkante und fällt ein Lot zu einer der Linien, die den Kreis unterteilen, so kann man den Sinus bzw. den Cosinus wie in der Abbildung gezeigt ablesen. Bei einem Winkel von 45° sind der Sinus und Cosinus gleich.
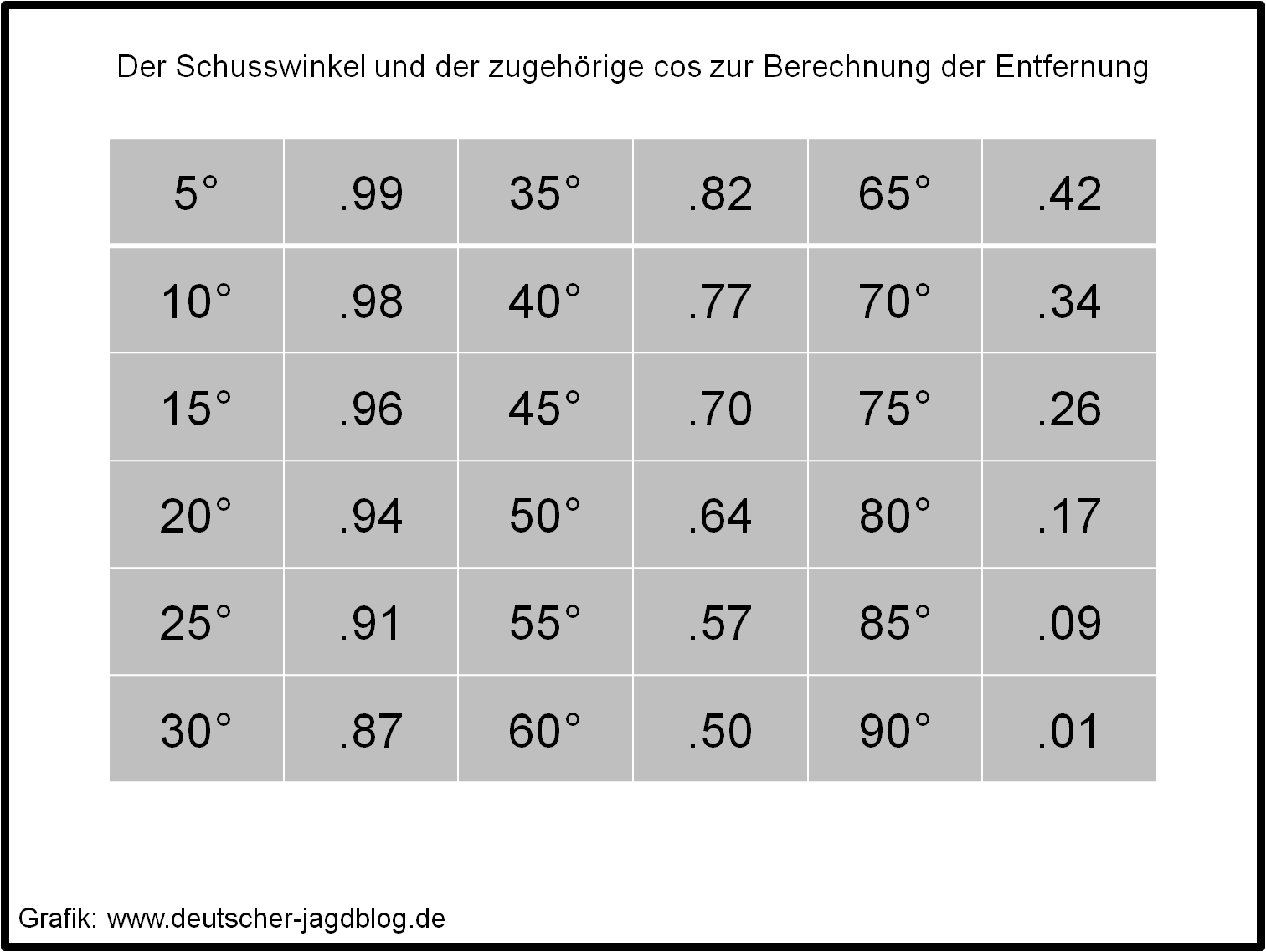
Für den Winkelschuss ist lediglich der Cosinus relevant, da er relativ zur Waagerechten berechnet wird. In der Realität müssen wir den Sinus und Cosinus nicht umständlich über eine solche Grafik ableiten, Scharfschützen benutzen hierfür entweder Winkeltabellen oder haben eine Libelle an der Optik befestigt, die den Cosinus anzeigt.
Um nun die relative Entfernung zu einem Ziel zu berechnen, muss man also den Winkel kennen, mit dem man schießt und man muss die Entfernung zum Ziel kennen. Angenommen man möchte eine Gams auf 150m in einem Winkel von 45° schießen: Man nehme einen Taschenrechner und drücke 45 cos, und multipliziert dann diesen Wert mit der real gemessenen Entfernung zur Gams. Als Hilfsmittel bietet sich dafür eine Laserentfernungsmesser an. Alternativ kann man auch den Cosinus von einer Libelle ablesen oder den entsprechenden Wert aus unserer Tabelle entnehmen. In der Abbildung 2 haben wir die Berechnungen für die Entfernungen 150m, 250m und 350m mit einem Winkel von 45° beispielhaft vorgegeben. Die Ergebnisse können hier leicht verständlich abgelesen werden.
Praxis
In der Praxis stellt sich dann natürlich die alles entscheidende Frage, ob auf Grundlage dieser Berechnung eine Veränderung des Haltepunktes notwendig ist?
Wir gehen mal davon aus, dass jeder seine Waffe nach unserer Anleitung zum Einschießen der Waffe eingeschossen hat. In diesem Fall haben Sie genaue Kenntnis über die GEE und die Pointblank Range Ihrer Waffe, was für den Schuss im Hochgebirgsrevier unerlässlich ist. Wir möchte Ihnen nun veranschaulichen, wie Sie mit Hilfe dieser theoretischen Grundlagen herausfinden können, ob und wie Sie den Haltepunkt verlegen müssen.
Aus diesem Grund haben wir nachfolgend eine Tabelle mit den ballistischen Grunddaten von der Munition 7,62 x 51 (.308 Winchester mit 168 grs) erstellt. Verschossen wird diese Munition aus einer Standardrepetierbüchse mit 24‘‘ Lauf, 8cm Visiererhöhung, die auf GEE 190m eingeschossen wurde (Pointblank range 225m). Der Tabelle können Sie entnehmen, dass das Projektil zum ersten Mal bei 45m die Visierlinie schneidet, auf 100m einen Hochschuss von 3,7 cm und auf 225m einen Tiefschuss von 4cm hat. Nehmen wir die tödliche Trefferzone einer Gams vom 8cm, kann ich auf der vollen Strecke von 35m bis 225m immer Zielmitte anhalten und werde immer innerhalb des Leben der Gams liegen.
Das vorangegangene Werte beziehen sich auf einen Schuss in der Horizontalen. Verändern Sie den Winkel verkürzen Sie auch die relative Distanz zum Ziel.
Nehmen wir nun an Sie schießen mit einem Winkel von 45° auf eine Distanz von 310m: In der Praxis würden nun viele Jäger einfach aufgrund der Entfernung versuchen tiefer anzuhalten. Aber ist das denn wirklich notwendig? Wenn man wie gezeigt die relative Distanz über den Cosinus berechnet, müssten Sie den Haltepunkt nicht verlagern. Der Cosinus von 45° ist 0,7, multipliziert mit 310m ergibt 224m. Zuvor haben wir festgestellt, dass die Beispielwaffe eine Pointblank Range von 225m hat, somit liegen wir trotz des Winkels immer noch innerhalb der tödlichen Trefferzone einer Gams. Demzufolge liegt der Schuss rechnerisch im Leben.
Allerdings lässt das mathematische Modell völlig außer Acht, dass man in einem steilen Winkel auf ein dreidimensionales Ziel schießt. Als Jäger wollen Sie die lebenswichtigen Organe des Stückes treffen und nicht lediglich in das Wild hineinschießen. Aus diesem Grund sind neben der genauen Kenntnis der Lage der inneren Organe des Wildes auch die Kenntnisse über die Besonderheiten beim Schießen auf dreidimensionale Ziele essentiell wichtig. Hierzu werden wir in Kürze einen Artikel veröffentlichen.
Fazit
Zusammenfassend kann man sagen, dass der Winkelschuss zwar Auswirkungen auf die Treffpunktlage hat, allerdings kaum jagdlich relevant ist. Schießt man lediglich auf Distanzen bis 150m und in einem Winkel unter 45° kann man in den meisten Fällen ohne Verlagerung des Haltepunktes schießen. Neben dem Winkel beim Schießen gibt es natürlich weitere Einflüsse, die man beim Schießen im Hochgebirge zu bedenken hat. Die Außenballistischen Faktoren wie Höhenlage, Luftdruck, Temperatur und den Wind haben in der Praxis dabei eine deutlich stärkeren Einfluss als die physikalischen Bedingungen eines Winkelschusses. Daher werden wir diese und weitere Themen in zukünftigen Artikeln vertiefen. Weiterhin wurde in der PIRSCH 14/ 2002 ein Artikel zu diesem Thema veröffentlicht, der dieses Thema ebenfalls beleuchtet und teilweise Grundlage für die hier dargestellten Sachverhalte ist.


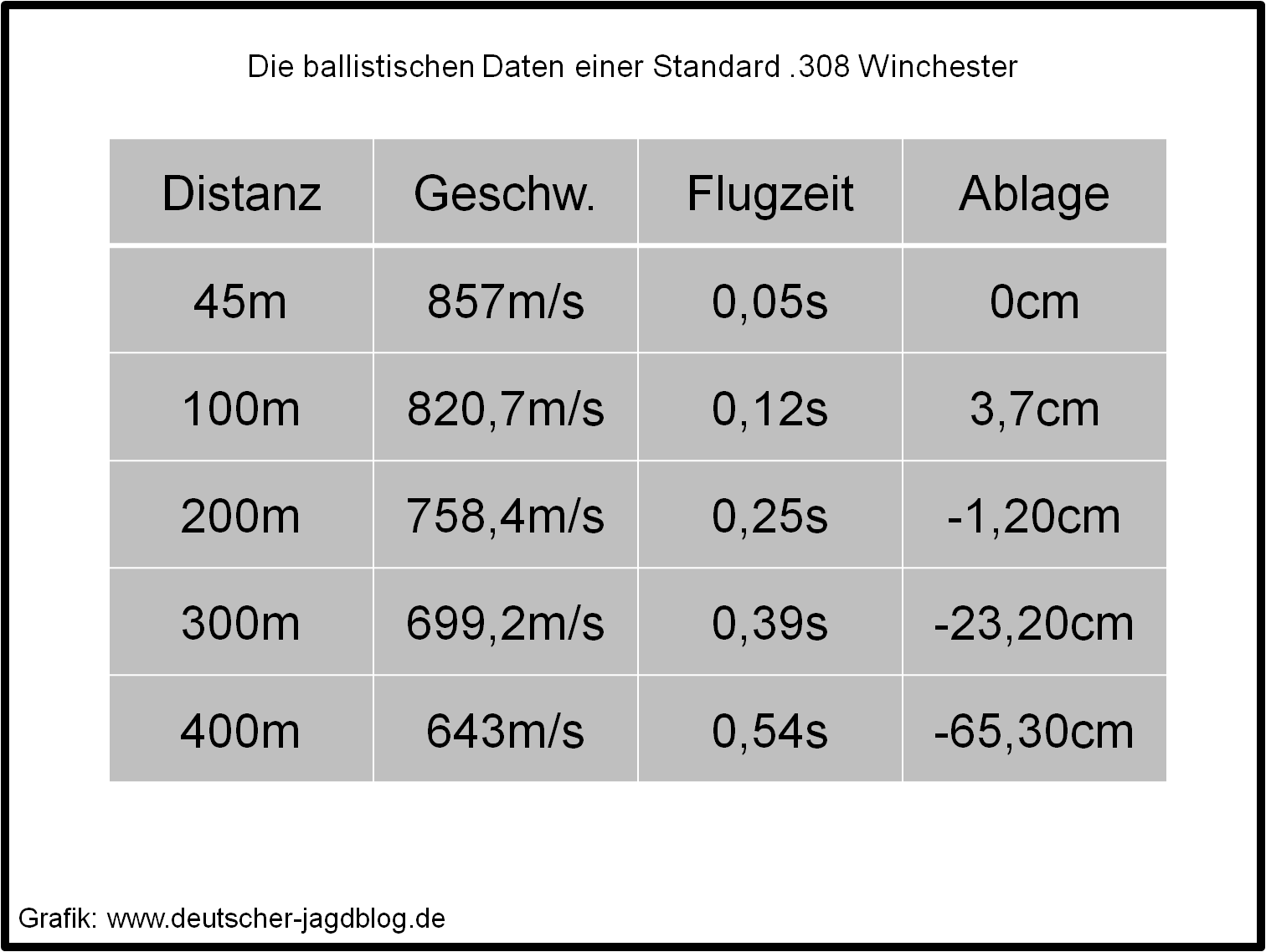








Welche 308 Win Patrone hat diese ballistischen Werte in der Tabelle?
Das war eine voreingestellte Patrone aus dem Ballistkrechner Strelok. Angeblich soll die eine standardisierte .308 darstellen.