Mythos Winkelschuss, Teil II

Vor kurzem hat uns ein Leser darauf angesprochen, dass sein neuer Laserentfernungsmesser andere Ablagen bei einem Winkelschuss anzeigt als sein altes Gerät. Woran kann das liegen? In diesem Artikel geben wir eine Antwort auf die Frage und zeigen gleichzeitig weitere präzise Rechenmethoden zum Thema Winkelschuss auf.

Der Fall wurde uns folgendermaßen geschildert: Er hat sich über eBay einen neuen deutschen Marken-Entfernungsmesser mit einem ballistischen Rechner gekauft, weil sein altes US-Fabrikat nicht mehr richtig funktionieren wollte. Leider musste unser Leser feststellen, dass sein neuer Entfernungsmesser, trotz gleicher ballistischer Werte für die Munition und die Waffe, ganz andere Werte für die Ablage anzeigte als der Alte. Die Frage an uns war nun, woran dies liegen kann und welchem Entfernungsmesser zu vertrauen ist?

Wie kommt es zu unterschiedlichen Ergebnissen?

Grundsätzlich kann man sagen, dass amerikanische Hersteller von ballistischer Software oder von Laserentfernungsmesser mit ballistischer Software, gerne nach dem Rechenverfahren der sog. „Marksman-Rule“, „Rifleman-Rule“ oder „Sniperchoice“ rechnen. Wir haben diese Form der Ermittlung von Ablagen bei einem Winkelschuss bereits letztes Jahr in unserem Artikel „Mythos Winkelschuss“ erläutert. Diese Art die Ablage bei einem Winkelschuss zu errechnen, ist ausreichend präzise für einen waidgerechten Schuss bis 250 m. Darüber hinaus wird die Formel zunehmend unpräziser. Das soll natürlich nicht bedeuten, dass nahezu alle Scharfschützen dieser Welt, die auf diese Weise ihre Ablagen ermitteln falsch rechnen, dennoch geht es technisch noch präziser.

Europäische Hersteller von Laserentfernungsmessern nehmen es etwas genauer mit der Berechnung von Ablagen und verwenden aus diesem Grund ein anderes Verfahren zur Bestimmung des Geschossfalls. Allerdings ist die „europäische Variante“ der Ablagenermittlung deutlich schwerer nachzuvollziehen und die praktische Umsetzung erfordert etwas mehr Vorbereitung. Für die meisten Jäger ist es daher empfehlenswerter die „Marksman Rule“ anzuwenden.

Alternative Möglichkeit die Ablage bei einem Winkelschuss zu ermitteln

Das Autorenteam Dr. F. Metzner und G. Holthaus haben in der Schweizer Jäger 01/ 2014, dieses Thema genauer unter die Lupe genommen und einen hervorragenden Artikel zu diesem Thema geschrieben. Grundsätzlich stimmen wir mit den dort publizierten Inhalten überein. Allerdings können wir aus Erfahrung sagen, dass die „Marksman-Rule“ bis 250 m sehr brauchbare und praxisnahe Ergebnisse liefert. Gepaart mit Erfahrung ist dies jagdlich vollkommen ausreichend, um waidgerecht zu schießen. Aber was ist nun der Unterschied der „Marksman-Rule“ zur europäischen Rechenmethode?

Abb. 1

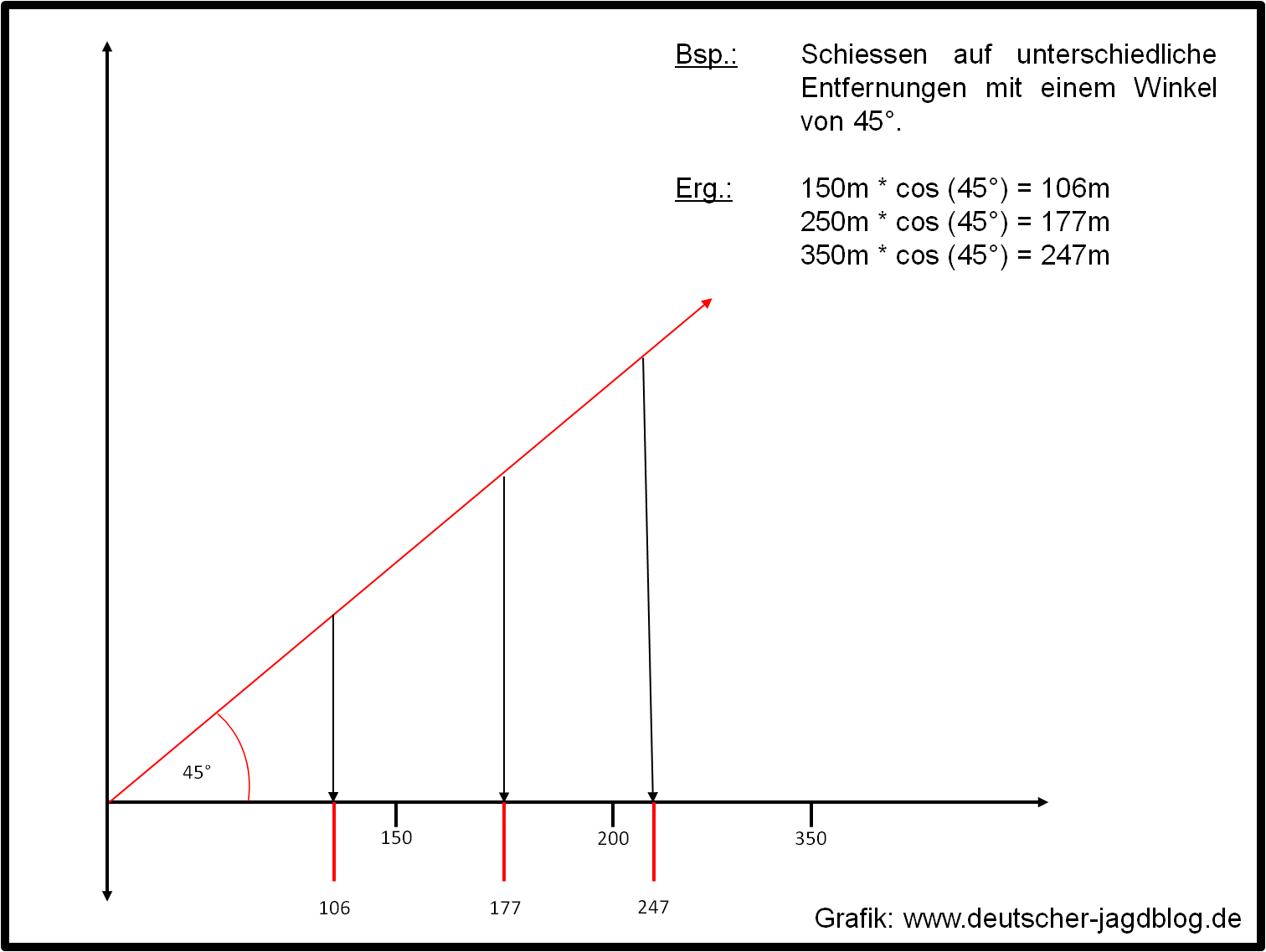
Die Marksman-Rule (s.a. Abb. 1) verfolgt den Ansatz, dass man lediglich den Cosinus des Winkels, mit dem man schießt, mit der Entfernung auf die man schießen möchte, multiplizieren muss. Somit erhält man die Entfernung mit der Anhaltemarke, mit der man das Stück anvisieren soll. Dem liegt der Gedanke zu Grunde, dass die Erdanziehung auf Grund der verkürzten Flugbahn nicht so lange auf das Geschoss einwirkt, wie bei einem horizontalen Schuss. Ein Schuss bergauf führt dementsprechend zu einem Hochschuss. Physikalisch ist dies aber nicht ganz richtig! Entscheidend für den Geschossfall ist die Zeit, in der die Erdanziehung auf das Geschoss wirken kann und diese ist beim Winkelschuss genauso lang wie bei horizontalen Schuss der gleichen Entfernung.

Abb. 2

Der entscheidende Unterschied des Winkelschuss gegenüber einem horizontalen Schuss liegt jedoch darin, dass der

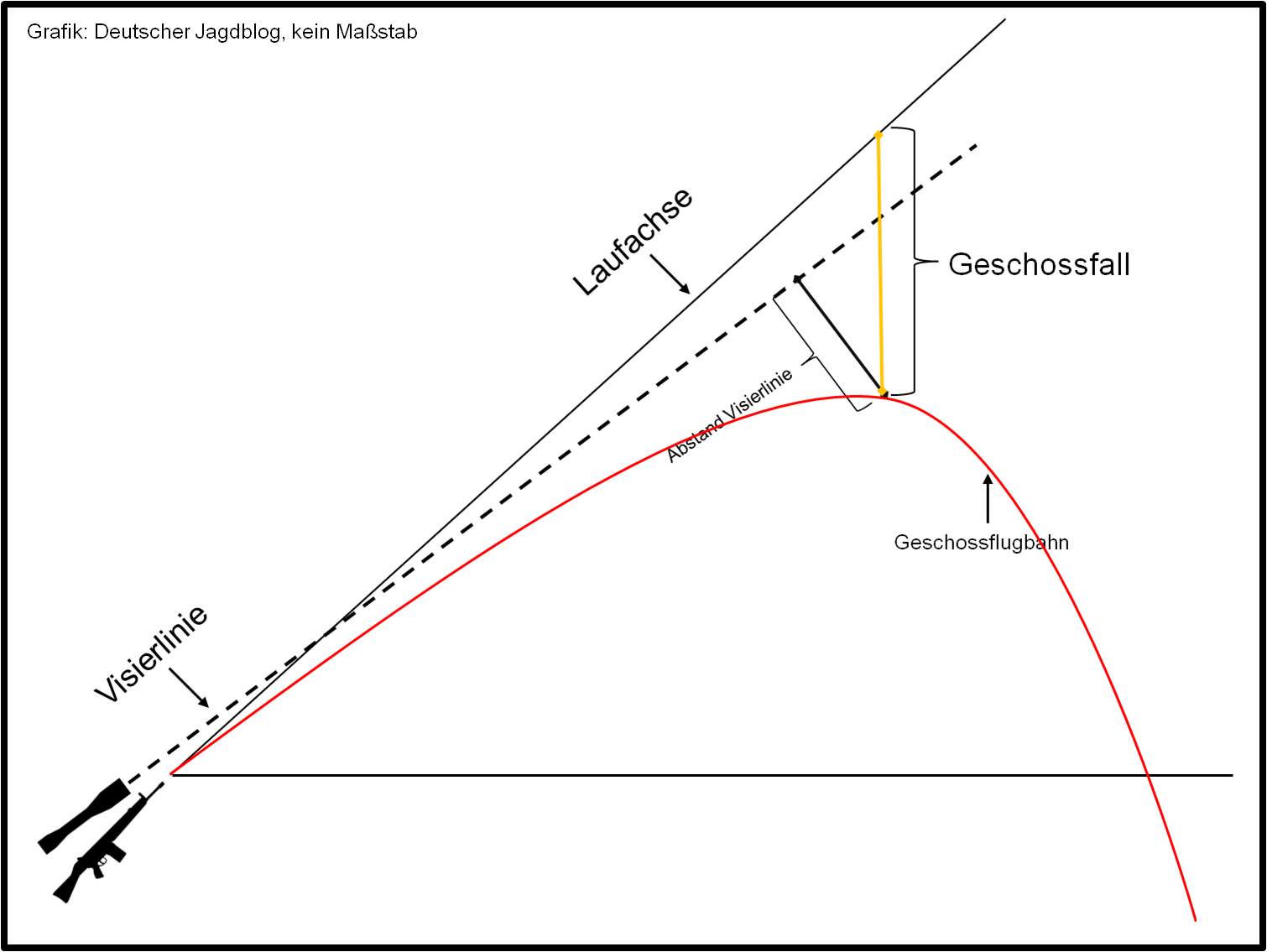
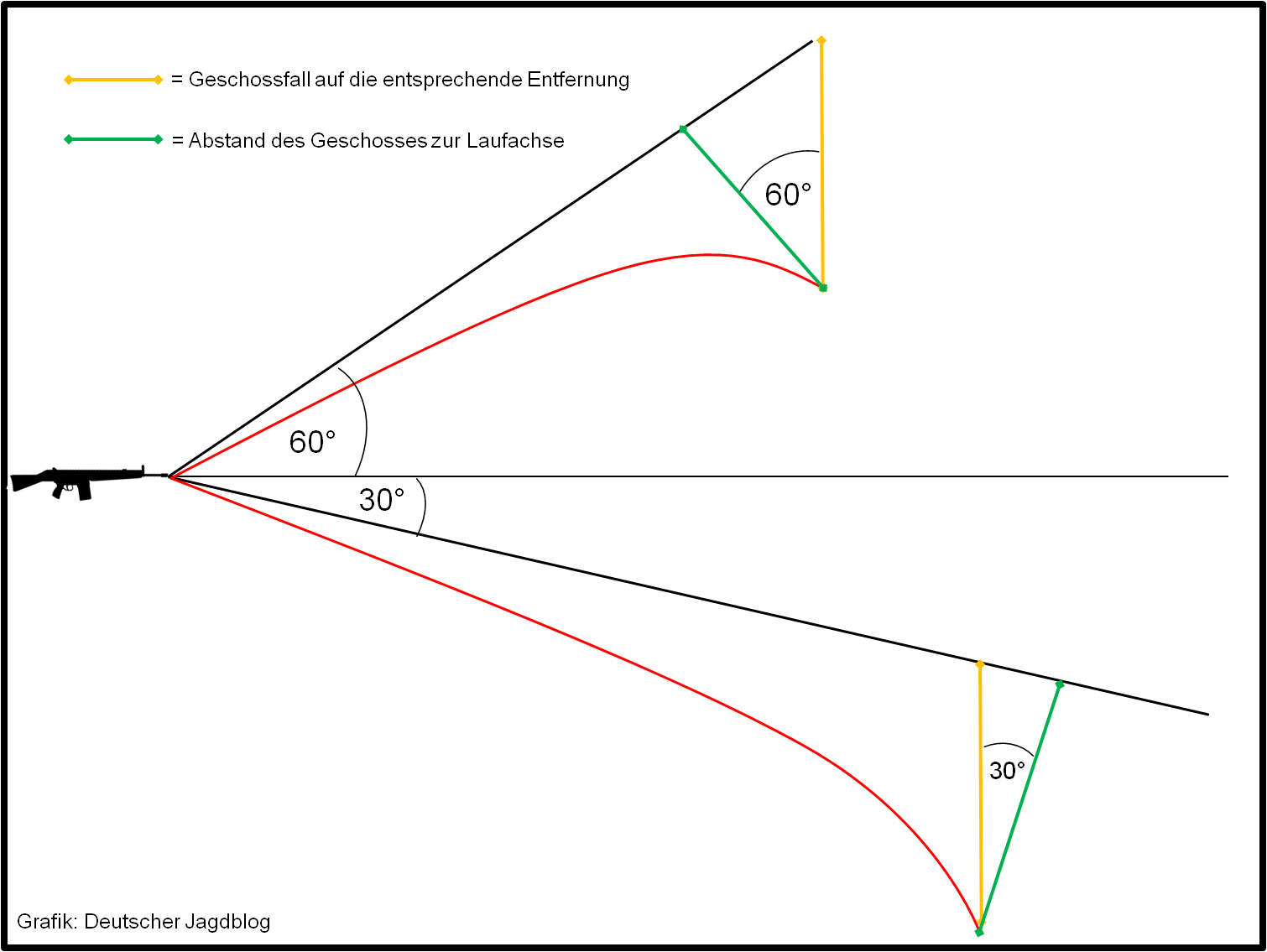
Schütze durch den steileren Winkel den Abstand der Visierlinie zur Geschossflugbahn verkürzt (s.a. Abb. 2). Hierdurch kommt es zu einem beobachteten Hochschuss (s.a. Abb. 3). Auf der Abbildung ist der Geschossfall (orange) und der senkrechte Abstand der Laufachse zur Geschossflugbahn (grün) dargestellt.

Abb. 3

Bei einem horizontalen Schuss sind Geschossfall und der Abstand der Laufachse zum Geschoss gleich groß. Neigt man nun die Visierlinie nach oben oder unten, verringert sich der Abstand der Laufachse zum Geschoss, der Geschossfall bleibt jedoch gleich. Der Abstand der Laufachse zum Geschoss lässt sich einfach errechnen, Formel:

Geschossfall (horizontal) x cos α

Bsp.: Unsere standard .308 Win hat auf die Entfernung von 200 m einen Geschossfall von 29,3 cm, wenn die Waffe auf 0 m eingeschossen wurde. Der Abstand der Laufachse bei einem Winkelschuss von 60° beträgt:

29,3 cm x cos (60) = 29,3 cm x 0,5 = 14,65 cm

Folglich sieht der Schütze einen Hochschuss von 14,65 cm und muss um diesen Wert tiefer anhalten, um fleck zu treffen. Da unsere Waffe in der Regel auf 100 m eingeschossen sind, muss man zusätzlich noch die Abweichung von der Flugbahn des Geschosses, bei der auf 100 m eingeschossenen Waffe, abziehen:

14,65 cm – 10,8 cm = 3,85 cm (Korrekturwert)

Die „Marksman-Rule“ hätte hier die Entfernung 200 m mit dem cos (60) multipliziert und wäre dann zu dem Schluss gekommen, mit dem einem Tiefschuss von 6,7 cm anzuhalten: Siehe gemäß Bsp. 1:

200 m x cos (60) = 200 m x 0,5 = 100 m

auf 100 m haben wir einen Tiefschuss von 6,7 cm

oder wir gehen von einer Waffe aus, die auf 100 m eingeschossen wurde, gemäß Bsp.2:

200 m x cos (60) = 200 m x 0,5 = 100 m

bei dieser Waffe haben wir auf 100 m einen Fleckschuss

In jedem Fall erhält man bei der Anwendung der „Marksman-Rule“ einen anderen Wert als bei der wesentlich präziser gerechneten Methode. Wir haben die „europäische Variante“ mit einem Ballistikprogram aus dem Internet nachvollzogen und sind zu dem Schluss gekommen, dass Sie rechnerisch wesentlich näher an der realen Geschossflugbahn ist als die „Marksman-Rule“.

Rechenmethoden in der Praxis

Im Grunde kommen Sie nicht daran vorbei eine Karte mit den Korrekturwerten für Ihre Waffe zu erstellen. Hierfür benötigen Sie ein Ballistikprogramm, z.B. das kostenlose Strelok oder JBM Ballistics.

Folgende Schritte müssen vollzogen werden:

Ermitteln des Geschossfalls Ihrer verwendeten Munition, wenn die Waffe auf 0 m eingeschossen wäre, für die Entfernungen 100 bis 400 m in 25m-Schritten. (Den Geschossabfall auf 0m können Sie beispielsweise behelfsmäßig ermitteln, indem Sie Ihre Waffe nah an die Wand halten, mit einer Taschenlampe durch die Optik leuchten und mit einer Laserpatrone im Lauf, den Abstand zwischen Laserpunkt und projektiertem Absehensmittelpunkt messen.)
Das Gleiche für die Flugbahn des Geschosses Ihrer Waffen mit der Entfernung, auf die Ihre Waffe eingeschossen wurde.
Bei Bedarf ermitteln Sie die Korrekturwerte zusätzlich in Klicks.
Im letzten Schritt errechnen Sie, wie oben beschrieben die Korrekturwerte für die Winkel zwischen 15° und 60° in 15er-Schritten.
Diese Werte notieren Sie in einer Exceltabelle drucken diese aus und laminieren sie.

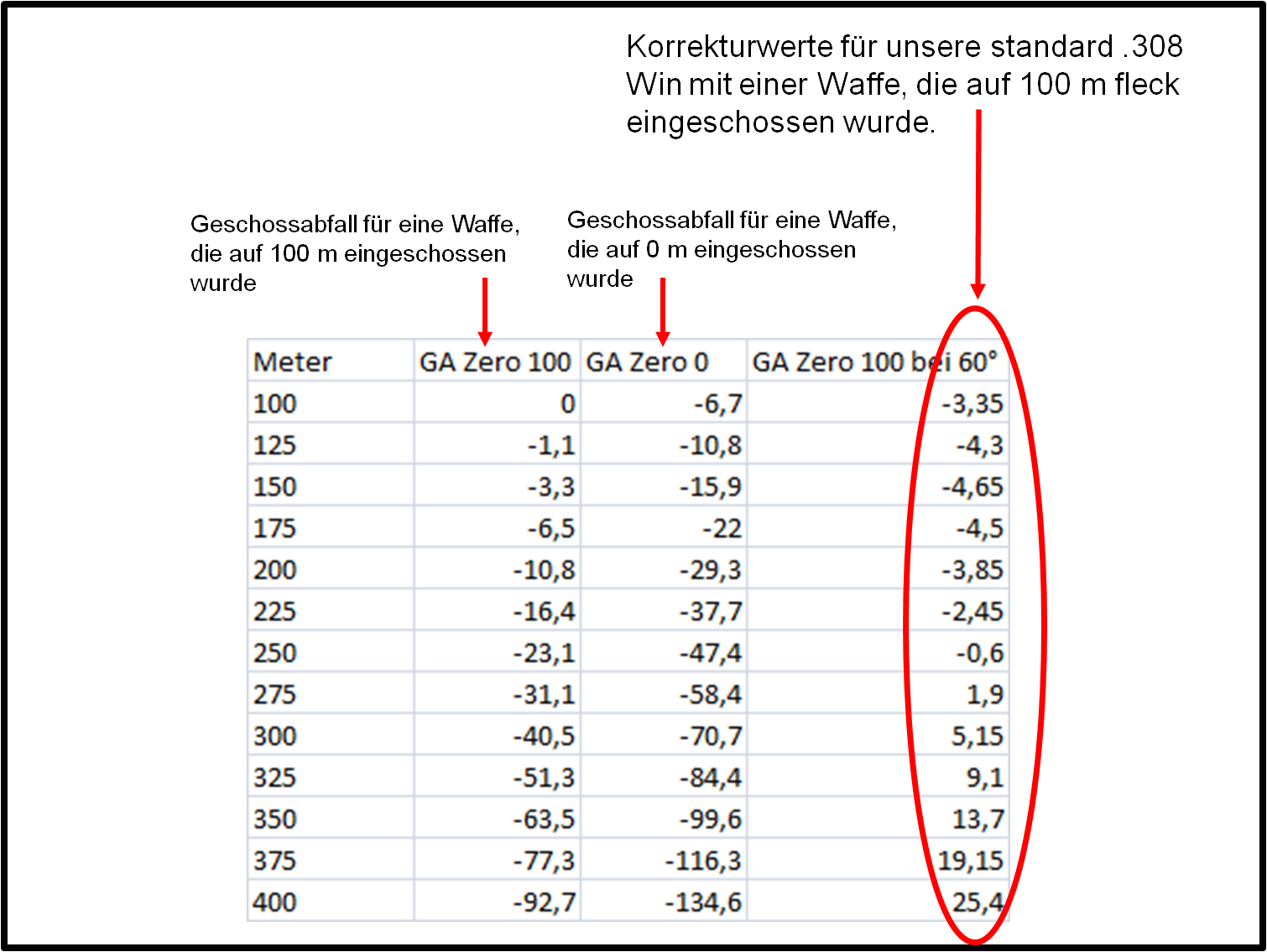
Wir haben dies für unsere Waffenkonfiguration in der nebenstehenden Tabelle getan. Aus Darstellungsgründen haben wir nur die Korrekturwerte für den Winkel von 60° aufgezeigt.

Wie kann man diese Tabelle interpretieren?

Nehmen wir die Spalte für 100 m. Unsere Waffe hat in der Horizontalen einen Tiefschuss von 0 cm, weil sie auf diese Entfernung eingeschossen wurde. Hätte wir die Waffe auf 0 m eingeschossen, so würde das Geschoss auf 100 m, 6,7 cm fallen. Schießt man nun mit dieser Waffe in einem 60° Winkel auf ein 100 m entferntes Ziel, muss man 3,35 cm oder 0,34 MIL tiefer anhalten, um Fleck zu schießen.

Bei der Ermittlung der Ablage auf diese Art und Weise kann es immer wieder zu Fehlern kommen, gerade wenn man unterschiedliche Ballistikprogramme verwendet oder die Korrekturwerte nicht in der Praxis überprüft. Die Tabelle beispielsweise gilt nur für unsere Waffe, Optik und Munition und ist auch nicht übertragbar. Es ist also schon Eigenleistung und ein wenig Akrebie von Nöten.

Auch wenn dieser Artikel sehr den theoretischen und mathematischen Hintergrund des Winkelschusses beleuchtet, hoffen, dass die Darstellung den Blick auf die Schießtechnik und deren Wichtigkeit für waidmännischen Schusses mehr in der Vordergrund rückt.